
the world of decimal
The sales tax on the disposable blue Bic pen set me back nineteen cents. That’s nine-plus-ten cents. It had taken twenty-six minutes to drive in mild traffic from downtown San Diego to the La Jolla bookstore, that’s twice-ten-plus-six minutes—a measurement kindly excluding the ages it took to find parking. As I write this, I have in front of me the thick tome of The Universal History of Numbers by Georges Ifrah. The highest page number is 634, that’s 63 tens of pages, plus an additional four. And of course 63 tens of pages means 6 tens (of tens) plus 3 (tens). When people communicate quantities, we organize large numbers into tens, then tens-of-tens if needed, and even tens-of-tens-of-tens if further needed, and so on. This we call the decimal system. Nearly any value flashing on TV, discussed in the board room, or settled at the stock market screams decimal. Even after your life runs its course, someone on your behalf will settle your final taxes in… decimal. We live and die in decimal.
The US national debt as of this morning in June 2023 was $31,467,099,921,028, a number 14 digits long. For every new dollar in debt, the rightmost digit grows by one. To grow past 9, that digit cycles back to 0, while the digit immediately to its left grows by 1. The same paradigm applies to all digits leftward. They grow to the highest available symbol, then they zero while spilling (“carrying”) to their left. This is how positional numeral systems work.
A medium American city like Richmond, Virginia can easily number 220,000 residents. By contrast the number of grains of sand from all the deserts and beaches on Earth is a much bigger number, a 7 followed by 18 zeros. If you were a resident of Richmond, and we divided all the grains of sand from all the Earth’s deserts and beaches to just the Richmonders, each of you would receive a number of sand grains roughly equal to the US national debt.
Counting systems work like this. You add, you divide, you multiply, you subtract. You do this by manipulating the digit positions, which in decimal are populated by the Hindu-Arabic symbols, e.g. 0,1,2,3,4,5,6,7,8,9.
Decimal is intuitive to humans, in large part because people have ten fingers. Fingers are prominent when, say, a street vendor hands to their customer a French baguette, a Mexican burrito, or an Algerian Mahjouba, as much as when the buyer pays in yen as in Japan, rand as in South Africa, or US dollars in the British Virgin Islands and America. As such, fingers can be roped into the conversation and the negotiation easily, to illustrate and to communicate counting. It makes sense that for everything to do with numbers we would use a system grouping items in tens, and multiples of tens.
Or so it would seem.
five lonely cups
Beneath the decimal radar, there is a parallel counting system we use in certain contexts. My first conscious exposure to it occurred when I attempted to provide a beautiful gift to my mom.
It was summer 1980. I flew back to Cyprus from my one and only camping trip near Athens, Greece. Toward the end of my two weeks there, the organizers shuttled us to Athens to visit the Parthenon, of course, and the Minion, a famous at the time nine-story shop in Athens — if you live in New York City, think the Macy’s of Athens at the time. I distinctly remember it was my first ever use of an escalator. For a bunch of kids living in tents in a rural area for several days, a nine-story building with escalators provided plenty of entertainment.
I purchased gifts for everyone in my immediate family. For my dad, I selected two ties. For my mom I got a set of five green and white Greek-coffee cups (similar size to espresso cups) with matching saucers.
“They’re gorgeous,” she exclaimed when she unwrapped the first one. Her face lit up “Wow! Thank you!”. After unwrapping the fifth one, she asked, “Is there a sixth cup?”
“Why? There’s 5 of us,” I explained, referring to my immediate family, of two parents and three kids, as if all five of us were eligible to drink coffee (which thankfully we were not.) At the time, I didn’t even notice how decimal a family of five was. Everything that can be divided by ten, can easily be divided by five as well. For example, if dividing ten bars of chocolate or ten bags of candy, each person would get two. Sweet deal!
Days later she explained to me why she asked that question. “Serving plates are usually sold in sets of six,” she said. “If I were the person ringing up a purchase made by someone your age, I would have suggested buying a sixth one to have a complete set. Then again, now we have a story to go with the cups!”
They became formal servings for rare occasions. But ingrained in my mind became the idea that you don’t buy serving plates, coffee cups, glassware, and whatnot in groups of five, even if you live in a family of five.
You don’t buy eggs in sets of five either. Why?
what's so special about twelve?
This morning while shopping for eggs, I needed to pick only one carton amongst dozens of options.
The variety was exhausting:
Cage Free Large Grade AA eggs
Pasture Raised Large Grade A eggs
Cage Free Large Brown Grade A eggs
Cage Free Large Grade AA White eggs
Large Cage Free Grade A Omega-3 eggs
Pasture Raised Large Brown Grade A eggs
Organic Pasture Raised Large Grade AA eggs
Organic Free Range Large Grade A Brown eggs
That’s a lot of eggs. What did all these eggs have in common, other than a fragile shell, a slimy egg white, and a yolk whose color might vary from pale yellow to marigold?
Nearly all came in sets of twelve.
I’ve baked, and occasionally unilaterally consumed, many a cake in my life yet none required a total of twelve eggs. Barely a fraction, in fact. Cookies like kourabiedhes, which are Greek barely-sweet butter cookies dusted with powdered sugar, often containing crushed almonds, or the quintessential American Chocolate Chip cookie never require twelve eggs. Not for home posology.
And this grouping into dozens doesn’t only apply to eggs.
Muffins, donuts, sandwich rolls, all come in half-dozens or dozens. The tomato paste I use comes in a twelve-pack. I barely ever use more than half a can in one go.
Why do so many foods come in dozens? Why not in tens and fives?
To the puzzlement of most earthlings, the United States continues to use a variant of the imperial system of units (feet and inches). Consider construction. Why does a foot have twelve inches? Would safety and earthquake resistance be compromised had the foot remained the same length but was divided into ten units, or seven units, or eleven units?
Why is a bouquet of roses made of twelve roses?
Why are there twelve hours in a day, and twelve hours in a night?
Why is beer sold in twelve-packs (and six-packs), but not in ten-packs and five-packs?
Why is a box of wine a twelve-pack?
Why is a jury in the United States made of twelve jurors?
Why are there twelve notes in an octave of Western music?
There must be something special about the number twelve.
religion
The cheapest answer to all of life’s big questions is to throw the towel into the ring while invoking God. Happy to temporarily oblige: the number twelve is special because God made it so.
But what do the world’s religions have to say about God’s relationship to twelve?
In Judaism we encounter the twelve tribes of Israel, the patriarch of each being a son of Jacob (who was later renamed Israel). All people of Jewish descent are believed to belong to one of these twelve tribes.
In Christianity, Christ notably selected twelve apostles (messengers) to spread Christ’s teachings posthumously. Moreover, the book of Revelations, the closing book of the New Testament, predicts that 12,000 people from each of the twelve tribes of Israel (a total of 144,000 people) are to be protected from certain judgments in the end days.
Centuries later in Islam, specifically in Twelver Shi'ism—the name should be a clue— comprising 85% of Shiites in the world, the number twelve has prominence. The number refers to the twelve Imams who are “both spiritual and political successors to the prophet Muhammad.”
Back to BCE times, Egyptians believed the sun god Ra journeyed through the underworld (“Duat”) every night. The underworld consists of, you guessed it, twelve regions signifying the twelve hours of the sun god's journey through it.
The ancient Greeks believed in the twelve Olympian gods who meddled in each other’s affairs and—wouldn’t it be boring otherwise—people’s too. Heracles (also known with the latinized Hercules) performed labors as penance for having killed his wife and children in a fit of madness, indeed a whole twelve such labors. And even earlier in Greek theogony, the Titans, children of Uranus (sky) and Gaia (earth) ruled the world before Zeus and his cohorts staged a successful coup. The number of those Titans? Twelve.
Far from the Mediterranean, the Nidanas in Buddhism are the links in a chain of origination (which I understand are a cause and effect sequence from ignorance to death). By now you wouldn’t be shocked to hear it from me: there are twelve Nidanas in Buddhism.
And in Hinduism, we encounter the twelve Adityas (offspring of Aditi, the goddess representing the infinity) who represent the twelve aspects of the Sun god Surya.
Despite all the aforementioned religions employing the number twelve in some or other capacity, it’s hard to discern a divine through line. The religious movements themselves are often at odds with each other on various dogmatic interests. And had there been such a divine through line, it would have served humanity better to prevent religious wars, than preserve holiness around the number twelve.
Besides, in none of the aforementioned religions does the number hold significant theological value.
In Christianity and Judaism the number twelve does not play a central role in doctrine (whereas in Christianity the number three does, as in the Holy Trinity).
In ancient Greek religion, numerology didn’t hold any particular significance. Numbers were not revered in the same manner that the twelve Olympian gods were revered. Besides, in addition to the twelve Olympian gods, gods such as Hades and Persephone, who did not reside on Olympus, were of equal significance.
Numerology hasn’t been central to Islamic belief either; the Quran does not treat twelve as a significant number.
And Buddhism too does not treat numbers as having special significance in themselves. Whereas there are Twelve Nidanas, the emphasis is on the dependent origination of phenomena, not the number itself. Of much greater importance in Buddhism is the Eightfold path and the Four Noble Truths, and even in those cases the emphasis is on the path and the truths, not the numbers eight and four.
Likewise, in Hinduism the number twelve appears a few times, but it plays the same role that the number does in the other religions—something that will become clear in the next section.
In conclusion, we do see a presence of the number twelve in the main religions. But as convenient as it might have been to attribute that presence to God or the Gods, such claim doesn’t track.
Whatever is responsible for, even in an economy thriving on the decimal system, you buying roses and eggs in sets of twelve, it probably had nothing to do with the heavens.
Or did it?
astronomy
Putting religion aside, there is a compelling reason why the number 12 became notable in human religions, a reason not depending on scripture, mysticism, divine inspiration, or any arbitrary human choice.
And such reason does reside in the heavens. It combines humankind’s need to search the skies for inspiration; and humankind’s need to sow and reap the earth, to generate food: the synergy of the lunar cycle and agriculture.
The exact time between two full moons is 29 days, 12 hours, 44 minutes and 2.8 seconds—about 29.5 days. If you do the calculations, you’ll find that twelve full lunar cycles fit in each year with about 11 days to spare. But thirteen lunar cycles would require 384 days, much more than even a leap year affords. (It is possible to have 13 full moons in a year but that’s because two full moons require only one lunar cycle. A new year with a full moon in its first few days will sport a 13th full moon before the end of the year.)
That there are twelve full lunar cycles in a year would not go unnoticed by any gluten-sowing farmer in ancient times. And for the last few thousand years, our hunter-gatherer ancestor largely transitioned to sowing-reaping (and eventually to remote-control flipping). Weather, the sky, and celestial phenomena became a compass for survival.
The number twelve, then, would be easy to associate with completeness, with wholeness, in agrarian societies whose eyes observed the lunar months for guidance on the seasons. A year is not complete without twelve full lunar cycles. Perhaps the tribes of Israel, Christ’s team of apostles, the imams of Twelver Shi’ism, the regions of Duat for the Egyptians, the gods-in-residence at Olympus, the links in the chain of origination in Buddhism, the twelve aspects of the Sun god in Hinduism — all these might have felt less complete had they not been twelve, without necessarily turning the number into a mystical quantity worth revering on its own.
The lunar cycles might explain the presence of the number twelve in religions, but as we saw earlier, such is not sufficient to make twelve prevalent in trade.
To find why twelve has become prevalent in trade, we need to follow the money.
economics
All trade requires a number system. In Western societies we are very used to base-10 numeric system, also known as decimal.
What this means is that we have ten (10) symbols 0,1,2,3,4,5,6,7,8,9 with which we represent the number zero followed by the first 9 numbers. To represent the tenth number, we revert to 0 at the rightmost digit, and introduce another digit just to the left: “10”. We then have 9+1 = 10. From there, we also get 10+1 = 11; 19+1 = 20; 99+1 = 100; 109+1 = 110; etc.
The prevalence of the decimal system is attributed to our having ten fingers. In The Universal History of Numbers, Ifrah writes “The importance of the hand, and more generally of the body in children's acquisition of arithmetic can hardly be exaggerated.”
If you have an apple for each of your ten fingers, you have ten apples. If you have two apples for each of your fingers, you have twenty apples. We are so used to the decimal system and its relation to our fingers, that it becomes impossible to imagine humans or anyone more comfortable with a system other than decimal. Even our conversation of other base systems has to engage the decimal system as a reference, in the process becoming ludicrously legalese so as to avoid confusion.
Consider this. Had I been born with eight fingers instead of ten, a base-8 octal system would make more sense to me. For my octal counting system, I could borrow the first 8 symbols you use for your base-10 system: 0,1,2,3,4,5,6,7. If I have an apple for every day of the week, I have (7)8 apples (the subscript8 denotes octal), which is the same symbol for (7)10 apples in decimal. (In decimal, by convention, we typically drop the subscript and the parentheses, except when we want to avoid ambiguity.)
(You don’t need to understand all the math and notation to get the gist here so feel free to skim through as needed.)
If I have two apples for every day of the week, I have (16)8 (read not as “sixteen” but as “one-eightsome, six”) apples in octal. In decimal, this would be (14)10 because one eightsome is (8)10, plus (6)10 equals fourteen (14)10. If I have three apples for every day of the week, the representation in octal would be (25)8 (“two-eightsome, five”) whereas in decimal the familiar twenty-one (21)10. In each of the three apple quantities 7, 14, 21, the count is the same but the two representations vary from octal to decimal.
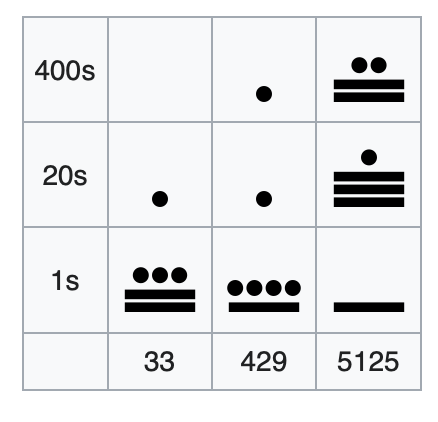
Some cultures did not evolve a decimal system. Some, like the Maya, used the vigesimal system which is base-20. Think of it as using both fingers and toes before having to “carry one” and switch to two digits. A big difference is that instead of “carry the one” to the left as we do in decimal when we go over ten, the Maya built their large numbers vertically. The number four-hundred twenty-nine (429)10 for example would be represented by the Maya as (119)20 (see middle column in image).
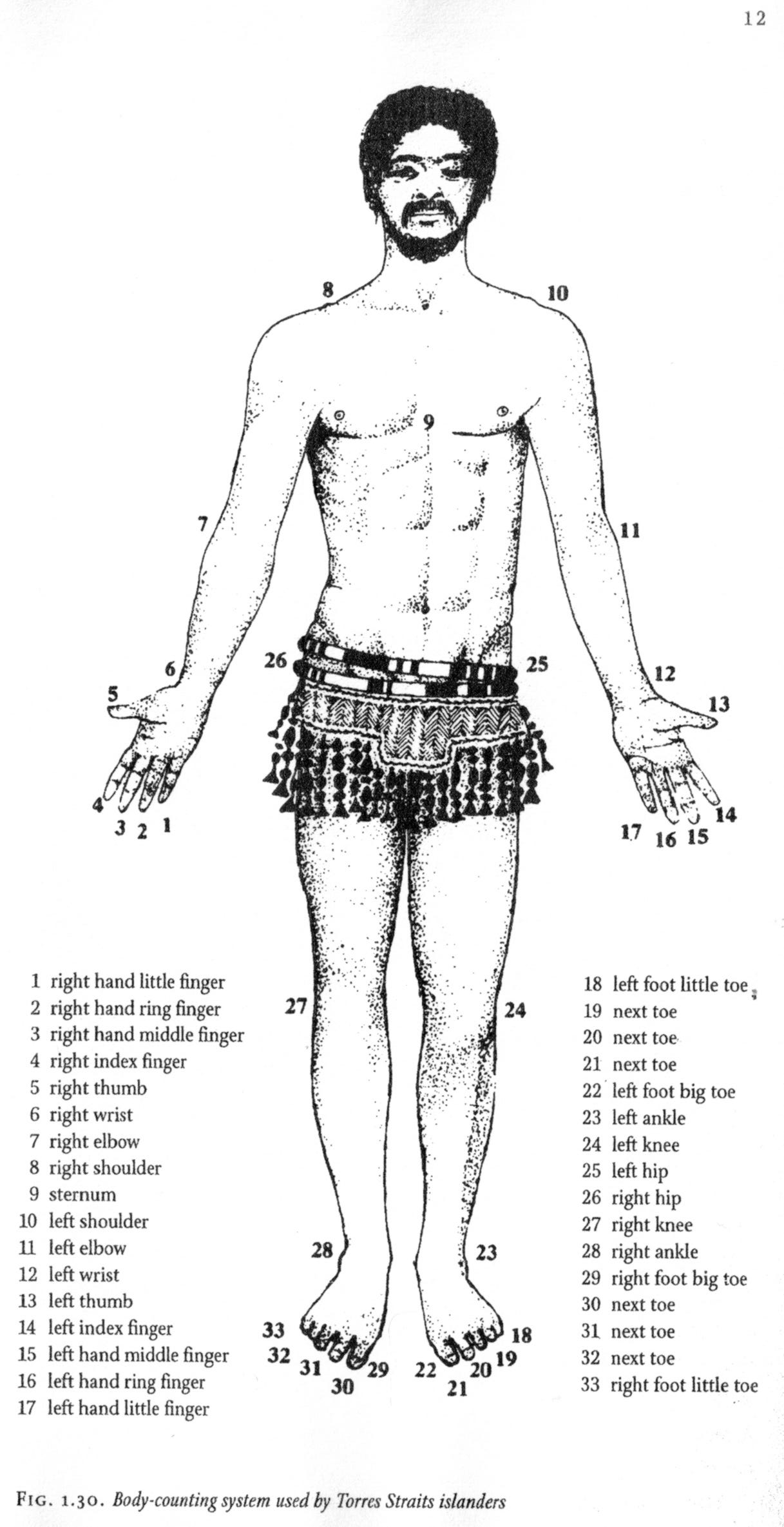
Some cultures even used their whole bodies when counting. According to Ifrah, the Cambridge Anthropological Expedition reported in the late 1800s that the Torres Straits Islanders “counted visually” up to thirty-three (33)10. Note that for a true base-33 system, they would need a symbol, or equivalent as you’ll see, for each number from 1 to 33, without having to resort to two-digit representaiton (as I just had to do for the number “33” because you and I communicate within a decimal system.)
Those symbols were specific parts of the body (see image.) For one of these islanders, having a wongai fruit—a fruit local to the islands of Torres Straits—for every day of the week (the number you and I call seven) meant they have “right elbow” wongai. Their largest single digit number would be “right foot little toe”. What do you get when you have “right wrist” wongai and I provide you another “left wrist” wongai? You have “left foot little toe” wongai.
Different contexts thrived on different “base” systems. You and I are used to decimal (base-10). Computers use binary (base-2). The Maya used vigesimal (base-20). Torres Straits islanders used base-33 (but not necessarily as a positional numeral system).
Which brings us to decimal (base-10) and duodecimal (base-12).
Is ten a good number for trade? Ten can be divided easily by one and by itself, but so can all whole numbers (like 7, 8, 52 etc). Most notably, ten can be divided by 2 and 5. And that’s it. If you collected ten roses, and you want to divide them amongst your 3 kids, tough luck. 3 is not a divisor of 10.
Twelve is more flexible. Twelve is divisible by 2,3,4,6 (and 1, as well as 12). If you have 12 oranges you can easily divide them amongst your 3 kids, your 4 cousins, your 2 parents.
If a foot were divided into ten units (instead of twelve) you could easily cut it in half, but not easily cut it in quarters without resorting to fractions. You cannot easily divide it by thirds either. But with a foot having 12 inches, all you have to do is find the marker at 4” and 8” and now you have that foot divided nicely into thirds. Find the marker at 6, and you got it divided in half. To divide in quarters, find the markers at 3”, 6”, 9”.
Twelve is much better suited for everyday division than ten. And that makes it better for trade.
Notice that division is another way of saying : arranging. If you have 12 eggs, you can divide (arrange) them into two rows of six eggs, or 3 rows of 4 eggs, etc. This matters for trade. For most of humanity (though perhaps less so today) packaging products for transfer must have been a challenge. Finding a transportation arrangement that works can make or break a business, much like throwing an arbitrary number of eggs in a bag is likely to result in scrambled eggs. Having options on how to arrange, how to divide, how to trade — that is what makes twelve so versatile.
Mathematicians call numbers with this property highly composite numbers (HCNs). The number 6 is an HCN because no smaller number than 6 can be divided by 2 and 3. The number 12 is an HCN because no number smaller than 12 can be divided by 2,3,4, (and 6).
But aren’t there better options than 12? After all, I can divide a dozen roses amongst 2,3,4,6, people, but not amongst 5.
There are other options, but learnability becomes an issue.
Consider the multiplication table for decimal. A helpful multiplication table for the decimal system has 9 rows and columns. Learners memorize that 3x7= 21 or that 8x9 = 72. Having memorized these basic transformations allows us to perform more complex transformations (such as 83 x 97) with procedural ease.
Multiplication tables have N-1 rows and N-1 columns, where N is the base. For decimal (base-10) we get a matrix of 81 squares to memorize. In actuality, we only need to memorize half the table due to the commutative property of multiplication (3x9 is the same as 9x3).
For the decimal system, we need to memorize 45 squares.
For duodecimal (base-12) we need to memorize 66 squares, so almost 1.5 times as much, but still doable.
By contrast, a base-33 counting system would require 528 squares to memorize.
The number higher than 12, that is divisible with all divisor of 12, and also divisible by 5, is the number 60. This number can be divided by 2,3,4,5,6, (and therefore by 10, 12, 15, 20, 30 as well). A true base-60 (sexagesimal) positional numeral system would need separate symbols for the first 59 digits. Even if we borrowed digits 1-9 from decimal, we’d need another 50 digits. We could borrow all English characters (26) and modern Greek characters (24) to make up such a set: 1,2,…,9,a,b,… z, α, β, … χ, ψ, ω. The number sixty-one (61)10 would be written as (11)60 whereas the number one-hundred-nineteen (119)10 would be written (1ω)60 .
Multiplication tables for such a system would be ultra complicated at 1770 squares to memorize compared to the decimal’s meager 45. You think memorizing 7x9 was challenging? Try memorizing 3 * ε, or η * j, on top of remembering 7x9. So even though 60 is conveniently divisible, sexagesimal is not suitable as a base for human arithmetic.
But no loss. Humanity wouldn’t leave the high-divisibility of the number 60 go to waste, even though it would be impractical to use base-60 as a positional numeral system. Rather, we brilliantly use 60 as the number of minutes in an hour. This means an hour can be easily cut in half (30 mins), in thirds (20 mins), in fourths (quarter hour), in fifths (12 minutes) and in sixths (10 minutes.)
All this is to bring us to the inescapable conclusions:
A base-60 system, is a fantastic number for trade because of its great divisibility, but 60 is not suitable as a base system because learning true base-60 arithmetic, with a multiplication table of 1770 boxes to be memorized, would be impossible. Any base over 60 would fare even worse.
On the other hand, base-ten is intuitive because of our ten fingers but isn’t the best number for trade in the ancient world. You can only practically divide it by two and five.
Base-twelve doesn’t have a much larger multiplication table than base ten, and twelve is a highly composite number, divisible by 2,3,4,6, (and 1, 12). This makes twelve an ideal number for trade math, for arranging items (such as eggs in a carton, or wine bottles in a box), or dividing length of 12 inches. Some cultures counted to 12 on one hand, by using the thumb to point to each of the 3 joints of the 4 remaining fingers, for a total of 12 joints. They used the other hand in a similar fashion to keep track of up to 12 dozens. With two hands, then, they could track counting up to 144. Can you do that in decimal?
The reason you buy eggs in dozens, roses in dozens, glassware in half-dozens or dozens, beer in half-dozens or dozens, wine in boxes of a dozen, donuts in dozens, and so forth is not religious or mystical at all.
It is efficiency.
It is pure economics.
the sixth cup
I remember at Sprouts Farmers Market, my scattered and rarely coherent mind imagined a toddler Carl Sagan looking at the egg display over his mother’s shoulder while she shops.
Mesmerized, he whispers: dozens and dozens!
The five coffee cups I gifted my mom were never amended to form a half-dozen set. In fact, arsonism took Minion out of business months after my purchases and despite efforts of the business to recover, it eventually closed down for good. If you want a complete set, get the number right the first time.
When I now buy items that form a set, not only do I ensure I have six or twelve, but often I entertain the thought of getting one extra piece which I safeguard in storage, in case one in my set breaks. I think of it as insurance toward having a full set. You either learn from your childhood mistakes, or you don’t. Sounds practical, though in the last few decades I had to replace an item in a set approximately these many times: zero.
conclusion
We live in a decimal world, but economics make duodecimal a more appealing counting system for trade. Had we been born with six fingers on each hand, decimal would never have stood a chance of dominating. Dinner rolls, eggs, roses, beers: they come in dozens because twelve has many divisors. US trade uses the foot divided into 12 inches, because on the job dividing is less cumbersome, making construction easier.
But technology has been taking over more and more of our menial tasks. In my research, I discovered there now exist cartons for ten, and even thirteen eggs. With technology it’s easier to break the mold of centuries, while remaining competitive.
Whatever competitive edge the duodecimal system possessed is waning. Perhaps it’s only fair that duodecimal may one day vanish, to the dismay of the Dozenal Society, a group committed to promoting the use of a base-12 system. As of this writing, their twitter account hasn’t posted anything since May 25, 2020, or as they might say May (21)12, (1204)12.
It would be fitting: even the name duodecimal is a nod to decimal.
Duodecimal then: less of a disrupter, more of an apologist. Yet common enough.
Acknowledgements: I appreciate you , , , for either providing early feedback and encouragement on the ideas put forth in the essay, or for reviewing and pointing out passages that could be improved. As always is the case, any remaining issues in the essay are mine and only mine to own.



...so much interesting info...the abstractness of the systems we use to control ourselves is such a rich pool and i appreciate you diving into this one and bringing back some trouts...a dozen fishes for the feast...
You mention the binary system, but only briefly. Considering the impact it has now wreaked upon civilization through computers, I feel it deserves a more thorough analysis.
In the late 1600s, Gottfried Wilhelm von Leibniz was the first western mind to grasp and employ the utility of the binary system – which he discovered through an ancient Chinese oracle, the I Ching. His motives were more philosophical than scientific, but he found the book's mathematical basis and implications an irresistible model for truth. Indeed, the I Ching was, and remains, a tool for people who seek answers to life's most fundamental questions. Leibniz was pursuing something more profound than simply promoting yin and yang into a revolutionary numerical engine that would animate the gadgets of the world.
That link — from the obscure ancient mystical to the ubiquitous modern practical — would be nothing more than the plot of an action adventure movie if it were not for the fact that computers, specifically artificial intelligence, are now on the verge of disrupting the entire human experience. Consulting the I Ching for insight into life a thousand years ago is one thing; relying on it for nuclear launch codes is quite another. Just what did Leibnitz discover?